(本小题满分14分) 已知数列
中，
，
. (1)求
; (2)求 的通项公式; (3)设Sn为数列
的前n项和,证明:
.
(本小题满分14分) 已知数列中，，. (1)求; (2)求 的通项公式; (3)设Sn为数列的前n项和,证明:.
(Ⅰ) 
(Ⅱ) 
（Ⅲ）见解析
1)由
,得: 2分
2)由(1)可归纳猜想:
………3分，
现用数学归纳法证明： ①当n=1时，显然成立；
②假设n=k(k∈N*)时成立，即，则：
n=k+1时：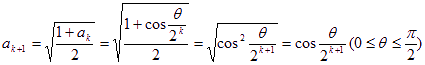
；
所以，n=k+1时，猜想也成立。故：由①②可知，对任意n∈N*,猜想均成立。…8分;
3)证明:设f(x)=x-sinx 
,则f`(x)=1-cosx≥0,
∴f(x)=x-sinx在
上是增函数. ∴f(x)≥f(0)=0,即sinx≤x .
又∵
,∴
,
∴
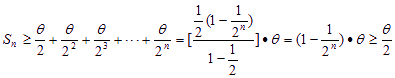…………14分。