(本题12分) 对于定义域为D的函数
，若同时满足下列条件：①
在D内单调递增或单调递减；②存在区间[
]
，使在[]上的值域为[]；那么把（
）叫闭函数。（1）判断函数
是否为闭函数？并说明理由；
（2）判断函数
是否为闭函数？若是闭函数，求实数
的取值范围。
(本题12分) 对于定义域为D的函数，若同时满足下列条件：①在D内单调递增或单调递减；②存在区间[]，使在[]上的值域为[]；那么把（）叫闭函数。（1）判断函数是否为闭函数？并说明理由；
（2）判断函数是否为闭函数？若是闭函数，求实数的取值范围。
解：（1）函数
上面单调递增，且
，所以是是闭函数。 （4分）
（2）函数
上单调递增，所以，如果为闭函数，则有
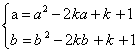，即方程
在
上有两个不等的实根。（8分）
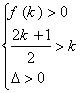，得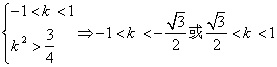
。 （12分）（或用韦达定理）