首页 / 如图1-2-4所示，有一弯成θ角的光滑金属导轨POQ，水平放置在磁感应

如图1-2-4所示，有一弯成θ角的光滑金属导轨POQ，水平放置在磁感应

如图1-2-4所示，有一弯成θ角的光滑金属导轨POQ，水平放置在磁感应强度为B的匀强磁场中，磁场方向与导轨平面垂直，有一金属棒MN与导轨的OQ边垂直放置，当金属棒从O点开始以加速度a向右匀加速运动t秒时，棒与导轨所构成的回路中的感应电动势是多少?

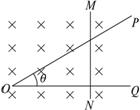
图1-2-4

答案

解析：由于导轨的夹角为θ，开始运动t秒时，金属棒切割磁感线的有效长度为：

L=stanθ=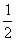

at2tanθ

据运动学公式，这时金属棒切割磁感线的速度为v=at

由题意知B、L、v三者互相垂直，有

E=BLv=B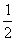

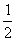
at2tanθ·at=Ba2t3tanθ

即金属棒运动t秒时，棒与导轨所构成的回路中的感应电动势是E=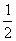

Ba2t3tanθ.

答案：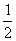

Ba2t3tanθ

相关题目

按流程图的程序计算，若开始输入的值为x=3，则输出的x的值
按流程图的程序计算，若开始输入的值为x=3，则输出的x的值是（ ） A．6              B．21         C．156                 D．231
已知实数 a， b，若 a＞ b，则下列结论错误的是 A． a-7＞
已知实数 a， b，若 a＞ b，则下列结论错误的是 A． a-7＞ b-7 B． 6+a＞ b+6 C．D． -3a＞ -3b
（16分）工业合成氨与制备硝酸一般可连续生产，流程如下：
（16分）工业合成氨与制备硝酸一般可连续生产，流程如下：（1）工业生产时，制取氢气的一个反应为：CO+H2O(g)CO2+H2。t℃时，往1L密闭容器中充入0.2molCO
生活中处处有化学。你知道下列化学原理吗？ （1）衣服上
生活中处处有化学。你知道下列化学原理吗？ （1）衣服上沾上油污时，可用洗涤剂或汽油除去，其中洗涤剂除油的原理是:                   
The farmer used wood to build a house ________ to store grain. A．with    
The farmer used wood to build a house ________ to store grain. A．with       B．in which        C．which                  D．in where
以下说法不正确的是( ) A.雄性动物从初情期开始产生精子 B.1
以下说法不正确的是( ) A.雄性动物从初情期开始产生精子 B.1个精原细胞可形成四个精子 C.精子在睾丸内形成时间为两个月左右 D.动物体型大的产生的精
设＝，则二项式展开式中含项的系数是              
设＝，则二项式展开式中含项的系数是                        
春季，河流流量显著增大的现象称为春汛,河流出现春汛的原
春季，河流流量显著增大的现象称为春汛,河流出现春汛的原因是多样的。读“哈尔滨气候资料表”（此数据亦可代表我国东北地区整体气候特征）和“

最新题目

下列说法中正确的是： A.场强为零的点，电势一定为零 B.电
溴酸钠(NaBrO3)是某种冷烫精的主要成分，对头皮有刺激作用，
有一种植物叫“苍耳”，当人们在草丛中行走的时候，裤脚
已知反比例函数（）的图象经过点（），则其函数关系式为__
Humans have sewn by hand for thousands of years. It was said that the first thr
下列说法中，正确的是A．△H>0表示放热反应，△H<0表示
设数列的前n项和为为等比数列，且， 。 （1）求数列和的通
被称为“开创建设有中国特色的社会主义新理论的宣言书”
在直角坐标系中，曲线的参数方程为（为参数，），以原点
 — Could you help me put up the signs on the wall? — ________       
实验小组研究盐酸、氢氧化钠的化学性质，做了如图甲所示
﹣2的相反数是（ ） A．2               B．﹣2     
关于三民主义的叙述，不正确的是（） A. 反映了资产阶级在
国家统计局透露，今后，“幸福感”将作为一项重要内容列
在等体积的pH值相等盐酸与醋酸溶液中，各加水稀释100倍，结
------I have just had my watch repaired. ------How much did they ____ for that?
在一个新鲜萝卜中挖一凹槽，在凹槽中放入浓盐水．一段时
下列这组图片与1992年后城市国有企业改革的哪项内容相关？
对于任意的直线l与平面a,在平面a内必有直线m,使m与l    
阅读下文，完成14—17题。（16分） 苦  瓜