错解1:∵函数y=tanx是增函数,又1＜2＜3＜4,∴tan1＜tan2＜tan3＜tan4.
错解2:∵2和3的终边在第二象限,∴tan2,tan3都是负数.∵1和4的终边分别在第一和第三象限,∴tan1,tan4都是正数.
又∵函数y=tanx是增函数,且2＜3,1＜4,∴tan2＜tan3＜tan1＜tan4.
教师可放手让学生自己探究问题的解法.发现错解后不要直接纠正,立即给出正确解法,可再让学生讨论分析找出错的原因.
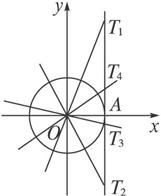
图6
解法一
:∵函数y=tanx在区间(
,
)上是单调递增函数,且tan1=tan(π+1),又
＜2＜3＜4＜π+1＜
,
∴tan2＜tan3＜tan4＜tan1.
解法二
:如图6,1,2,3,4的正切函数线分别是AT1,AT2,AT3,AT4,∴tan2＜tan3＜tan4＜tan1.
点评
:本例重在让学生澄清正切函数单调性问题,这属于学生易错点.把正切函数y=tanx的单调性简单地说成“在定义域内是增函数”是不对的.