(本题满分12分)平面直角坐标系中,![]() 为坐标原点,给定两点
为坐标原点,给定两点![]() ,点
,点![]() 满足
满足 ![]() ,其中
,其中![]() ,且
,且![]() . (1)求点
. (1)求点![]() 的轨迹方程;(2)设点
的轨迹方程;(2)设点![]() 的轨迹与双曲线
的轨迹与双曲线![]() 交于
交于![]() 两点,且以
两点,且以![]() 为直径的圆过原点,求证:
为直径的圆过原点,求证:![]() 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于![]() ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
(本题满分12分)平面直角坐标系中,![]() 为坐标原点,给定两点
为坐标原点,给定两点![]() ,点
,点![]() 满足
满足 ![]() ,其中
,其中![]() ,且
,且![]() . (1)求点
. (1)求点![]() 的轨迹方程;(2)设点
的轨迹方程;(2)设点![]() 的轨迹与双曲线
的轨迹与双曲线![]() 交于
交于![]() 两点,且以
两点,且以![]() 为直径的圆过原点,求证:
为直径的圆过原点,求证:![]() 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于![]() ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
(Ⅰ) ![]() (Ⅱ) 2 (Ⅲ)(0,1
(Ⅱ) 2 (Ⅲ)(0,1![]()
解.(1)设![]()
![]() ,因为
,因为![]() ,则
,则![]()
所以![]() 即点
即点![]() 的轨迹方程为
的轨迹方程为![]() --- 3分
--- 3分
(2) 明:由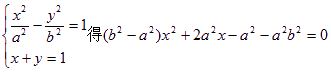
设![]() ,则
,则![]()
因为以![]() 为直径的圆过原点,所以
为直径的圆过原点,所以![]()
化简得![]() ----8分
----8分
(3) 因为![]() ,所以
,所以![]() 因为
因为![]()
所以双曲线实轴长的取值范围是(0,1![]() ——12分
——12分