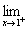试讨论当a、b为何值时,f(x)在x=1处可导. 
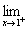试讨论当a、b为何值时,f(x)在x=1处可导. 分析：本题考查分段函数在接点处的导数.需依据导数的定义,分别求解此函数在接点处的左导数与右导数.
解：要使f(x)在x=1处可导,则f(x)在x=1处必连续,则+f(x)=f(1),即a+b=1.
又若
存在,则当x=1时,有
=
.
∵
=
=
(2+Δx)=2,
=
∴b=2,a=-1,
即当a=-1,b=2时,函数f(x)在x=1处可导.