，P在平面ABC内的射影为BF的中点O。（Ⅰ）证明
⊥
；
（Ⅱ）求面
与面
所成二面角的大小。
，P在平面ABC内的射影为BF的中点O。（Ⅰ）证明⊥；
（Ⅱ）求面与面所成二面角的大小。
本小题主要考查直线与平面的位置关系、二面角及其平面角等有关知识，考查思维能力和空间想象能力；考查应用向量知识解决立体问题的能力.
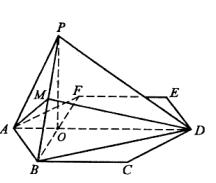
方法一
连结,则易知与的交点为
(Ⅰ)证法1：
又
平面
，
由三垂线定理得
.
证法2：
平面
平面
.
（Ⅱ）解：设
为
的中点，连结
在
中，
斜线
在平面
内的射影为
由三垂线定理得
又
平面
平面
因此，
为所求二面角的平面角.
在正六边形
中，
在Rt
中，
在Rt
中，
则
在
中，由余弦定理得
因此，所求二面角的大小为
方法二
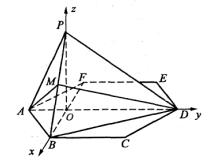
由题设条件，以
为原点建立空间直角坐标系
，如图.由正六边形的性质，可得
在Rt
中，
故
因而有
（Ⅰ）证明：因
故
所以
（Ⅱ）解：设
为
的中点，连结
，则
点的坐标为
因此，
为所求二面角的平面角.
因此，所求二面角的大小为