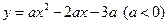 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.(1)求A、B的坐标;
(2)过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;
(3)在第(2)小题的条件下,直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
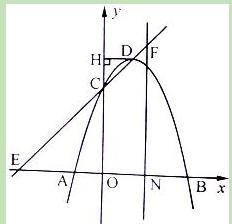
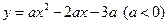 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
 ,
, ,
,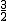 ,0)
,0)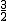 ,
,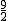 ),EN=
),EN= 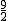 ,
,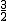 ,m),则FM=
,m),则FM= 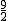 -m,
-m,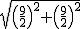 =
= 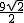 ,MQ="OM="
,MQ="OM=" 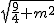
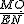 =
= 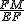 ,
,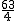 ,
,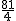 =
= 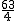 +
+ 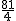
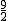 )2=
)2= 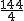
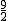 ="±"
="±" 
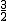 ,m2="-"
,m2="-"  ,
,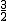 ,
,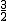 ),M2(
),M2(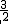 ,-
,-  ).解析:
).解析: