(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
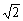
(Ⅰ)求MN的长;
(Ⅱ)当a为何值时,MN的长最小;
(Ⅲ)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
(18)本小题主要考查线面关系、二面角和函数极值等基础知识,考查空间想象能力和推理论证能力.
解:(Ⅰ)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形,∴MN=PQ.
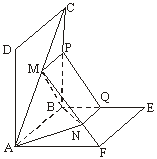
由已知,
CM=BN=a,CB=AB=BE=1,
∴AC=BF=![]()
![]()
即CP=BQ=![]()
∴MN=PQ=![]()
=![]()
=![]()
(Ⅱ)由(Ⅰ),
MN=![]()
所以,当a=![]()
即M、N分别移动到AC、BF的中点时,MN的长最小,最小值为![]()
(Ⅲ)取MN的中点G,连结AG、BG,
∵AM=AN,BM=BN,G为MN的中点
∴AG⊥MN,BG⊥MN,∠AGB即为二面角α的平面角,
又AG=BG=![]()
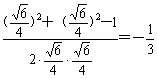 .
.故所求二面角α=arccos(-![]()