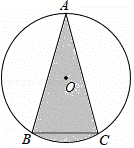
如图，⊙O中，
＝
，∠ACB＝75°，BC＝2，则阴影部分的面积是（ ）
A．2+
π B．2+
+π C．4+π D．2+
π
如图，⊙O中，＝，∠ACB＝75°，BC＝2，则阴影部分的面积是（ ）
A．2+π B．2++π C．4+π D．2+π
A【分析】连接OB、OC，先利用同弧所对的圆周角等于所对的圆心角的一半，求出扇形的圆心角为60度，即可求出半径的长2，利用三角形和扇形的面积公式即可求解；
【解答】解：∵
＝
，
∴AB＝AC，
∵∠ACB＝75°，
∴∠ABC＝∠ACB＝75°，
∴∠BAC＝30°，
∴∠BOC＝60°，
∵OB＝OC，
∴△BOC是等边三角形，
∴OA＝OB＝OC＝BC＝2，
作AD⊥BC，
∵AB＝AC，
∴BD＝CD，
∴AD经过圆心O，
∴OD＝
OB＝
，
∴AD＝2+，
∴S△ABC＝
BC•AD＝2+
，S△BOC＝
BC•OD＝，
∴S阴影＝S△ABC+S扇形BOC﹣S△BOC＝2++
﹣＝2+
，
故选：A．
【点评】本题主要考查了扇形的面积公式，圆周角定理，垂径定理等，明确S阴影＝S△ABC+S扇形BOC﹣S△BOC是解题的关键．