(10分)如图,已知直角梯形ABCD中,AD//BC, DC⊥BC,AB=5,BC=6,∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.

(1)当BO=AD时,求BP的长;
(2)在点O运动的过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
(3)在点O运动的过程中,以点C为圆心,CN为半径作⊙C,请直接写出当⊙C存在时,⊙O与⊙C的位置关系,以及相应的⊙C半径CN的取值范围.
(参考数据:cos53°≈0.6;sin53°≈0.8;tan74°
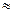
3.5)
解:(1)∵AD//BC,BO=AD
∴四边形AB0D为平行四边形-------------------------------------------------------------------------1分
∴AB//OD,∠COD=∠ABO=53°,DO=AB=5
在Rt
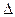
OCD中,
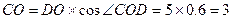
, BO=BC-CO=3.-----------------2分
在RtPOB中,BO=PO, ∴BP=

-------------------------------------------3分
(2)不存在.---------------------------------------------------------------4分
如图,过A点作AE⊥BC交BC于E点.若BP = MN,则△BOP≌△MON--------------------------------5分

∴∠BOP=∠MON=180°- 2∠B = 74°
DC=AE=

-------------------------------------------------------------------------6分
在Rt
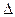
OCD中,

. BO=BC-CO=
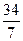
在△POB中,BP=
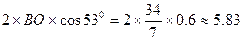
因为AB=5,所以BP>AB.
又因为P点在边AB上,即BP<AB.
所以BP与MN不可能相等.--------------------------------------------------------------------------- 8分
(3)当

⊙O与⊙C外切,CN 取值范围为 0< CN < 6 ------------ 9分
当

⊙O与⊙C内切,CN 取值范围为

------------- 10分解析:
略

 3.5)
3.5) 
 3.5)
3.5)  OCD中,
OCD中,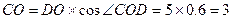 , BO=BC-CO=3.-----------------2分
, BO=BC-CO=3.-----------------2分 -------------------------------------------3分
-------------------------------------------3分
 -------------------------------------------------------------------------6分
-------------------------------------------------------------------------6分 OCD中,
OCD中, . BO=BC-CO=
. BO=BC-CO=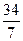
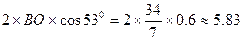
 ⊙O与⊙C外切,CN 取值范围为 0< CN < 6 ------------ 9分
⊙O与⊙C外切,CN 取值范围为 0< CN < 6 ------------ 9分 ⊙O与⊙C内切,CN 取值范围为
⊙O与⊙C内切,CN 取值范围为  ------------- 10分解析:
------------- 10分解析: