设函数
.
(Ⅰ)求函数
的单调区间;
(Ⅱ)当
时,不等式
恒成立,求实数
的取值范围;
(Ⅲ)关于
的方程
在
上恰有两个相异实根,求
的取值范围.
设函数.
(Ⅰ)求函数的单调区间;
(Ⅱ)当时,不等式恒成立,求实数的取值范围;
(Ⅲ)关于的方程在上恰有两个相异实根,求的取值范围.
递增区间是
;递减区间是
; 
;
( I)函数定义域为
. 
.
由
得
或
;
由
得
或
.
因此递增区间是;
递减区间是.
(Ⅱ)由(1)知,在
上递减,在
上递增.
又
且
,
所以时,
.
故时,不等式恒成立.
(Ⅲ)方程
即
.
记
,则
. 由
得
或
;
由
得
.
所以
在
上递减,在
上递增.
为使在上恰好有两个相异的实根,只须
在
和
上各有一个实根,于是有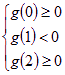
,解得
故实数的取值范围是.