【答案解析】（1）4×104m/s．（2）π×10-5s，垂直地打在BC边的中点．（3）分析过程如上所述．解析解：（1）粒子从P极板进入电场后，做加速运动，有： qU＝mv2−mv02 v=4×104m/s （2）粒

【答案解析】（1）4×10⁴m/s．（2）π×10^-5s，垂直地打在BC边的中点．（3）分析过程如上所述．解析解：（1）粒子从P极板进入电场后，做加速运动，有：
qU＝mv²−mv₀²
v=4×10⁴m/s
（2）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力：
qvB＝m故R＝＝0.8m
所以垂直地打在BC边的中点．
粒子在磁场中运动的周期为
T＝偏转角为90°，
所以粒子在磁场中运动的时间为t＝T＝×10⁻⁴s＝π×10⁻⁵s
（3）当粒子以反向最大电压进入电场时，粒子不能穿过Q点进入磁场．
t=0时刻射入的粒子，没有经过加速，粒子将以v₀=2.0×10⁴m/s从O点射入磁场，
R_min＝＝0.4m．恰好打到C点
因此OC边可以全部打到．
当粒子以正向最大电压加速进入电场中，根据动能定理：
qU_m＝mv_m²−mv₀²
最大速度v_m＝10⁵m/s
R_max＝＝2m
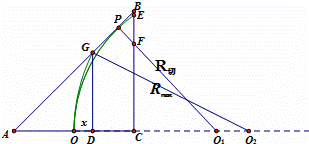
若粒子与AB边相切飞出，如图所示，根据几何关系可得：
BF+FC=a，
R_切=PF+FO₁，可得：
R_切＝0.8×(+1)m＜R_min
由以上三个半径关系可知，粒子从BC 和AB边飞出．
若恰好与AB相切的粒子打在BC边E，离C点的距离为：0.8在EC之间均有粒子飞出
与AB边相切的切点P到B点的距离为：0.8(−1)m
当粒子以最大速度进入磁场时，粒子将从AB边界的G点飞出，设OD之间的距离为x，则：
GD=AD=x+,O₂=R_max-x，
根据几何关系可得：(+x)+(R_max−x)²＝R_max²
可得x=0.4m
最大速度粒子从AB边上射出点G到B点的距离为：0.4m
在GP之间均有粒子飞出．