еҰӮжһңf(x)=sin(2x+ПҶ)дё”еҮҪж•°f(x)+fвҖІ(x)дёәеҘҮеҮҪж•°пјҢfвҖІ(x)дёәf(x)зҡ„еҮҪж•°пјҢеҲҷtanП
еҰӮжһңf(x)=sin(2x+ПҶ)дё”еҮҪж•°f(x)+fвҖІ(x)дёәеҘҮеҮҪж•°пјҢfвҖІ(x)дёәf(x)зҡ„
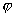
еҮҪж•°пјҢеҲҷtanПҶ=_____________.
зӯ”жЎҲпјҡ
-2В гҖҗи§ЈжһҗгҖ‘жҚ®йўҳж„ҸеҸҜеҫ—пјҡf(x)+fвҖІ(x)=sin(2x+
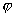
)+2cos(2x+
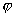
)дёәеҘҮеҮҪж•°,з”ұеҘҮеҮҪж•°е®ҡд№үеҸҜеҫ—пјҡsin(-2x+
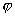
)+2cos(-2x+
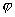
)=-[sin(2x+
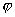
)+2cos(2x+
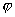
)]ж•ҙзҗҶеҫ—пјҡcos2x(2cos
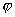
+sin
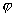
)=0,ж•…еҝ…жңү2cos
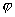
+sin

=0еҚіtan
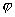
=-2.