（08年聊城市四模理） （12分） 已知点G是△ABC的重心，A（0，－1），B（0，1）. 在x轴上有一点M，满足
，
（若△ABC的顶点坐标为
，则该三角形的重心坐标为
.
（1）求点C的轨迹E的方程；
（2）若斜率为k的直线l与（1）中的曲线E交于不同的两点P、Q，且
，试求斜率k的取值范围.
（08年聊城市四模理） （12分） 已知点G是△ABC的重心，A（0，－1），B（0，1）. 在x轴上有一点M，满足，（若△ABC的顶点坐标为，则该三角形的重心坐标为.
（1）求点C的轨迹E的方程；
（2）若斜率为k的直线l与（1）中的曲线E交于不同的两点P、Q，且，试求斜率k的取值范围.
解析：（1）设C（x，y），则
.………………………………………………1分
，
………………4分
（2）①当k=0时，l与椭圆C有两个不同的交点P、Q，
根据椭圆的对称性，有
，符合题意.………………………………5分
②当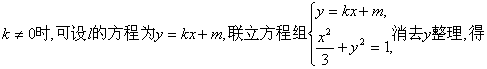
（*）
即1+3k2－m2>0. （**）……………………………………………………8分
、x2是方程（*）的两相异实根.
则PQ的中点N（x0，y0）的坐标是
即
），又
……10分
将
代入（**）式，得
综上①②，得k的取范围是（－1，1）.…………………………………………12分