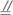
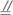
证法一:作正方形BCC1B1和CC1D1D，并连结A1B1和AD.
∵AA1CC1
BB1
DD1,且AA1⊥AB，AA1⊥A1D1，
∴ABB1A1和AA1D1D都是正方形，且ACC1A1是平行四边形.
故它们的对应边平行且相等.
∵△ABC≌△A1B1C1,
∴A1B1⊥B1C1.
同理，AD⊥CD.
∵BB1⊥AB,BB1⊥BC,∴BB1⊥平面ABC.
同理，DD1⊥平面ACD.
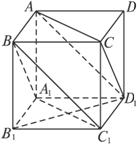
∵BB1∥DD1,
∴BB1⊥平面ACD.
∴A、B、C、D四点共面.
∴ABCD为正方形.
同理，A1B1C1D1也是正方形.
故ABCD—A1B1C1D1是正方体.
易知A1C1∥AC，
∴A1C1∥平面ACD1.
同理，BC1∥平面ACD1，
∴平面A1BC1∥平面ACD1.
证法二:证ABCD—A1B1C1D1是正方体，同上.
连结B1D、B1D1，则B1D1是B1D在底面ABCD上的射影，
由三垂线定理知B1D⊥A1C1，同理可证B1D⊥BA1，
∴B1D⊥平面A1BC1.
同理可证，B1D⊥平面ACD1，
∴平面A1BC1∥平面ACD1.