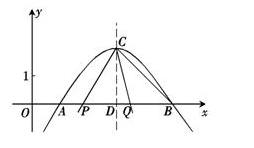
如图，在平面直角坐标系xOy中，抛物线
与x轴交于A（1，0）、B（5，0）两点．
1.求抛物线的解析式和顶点C的坐标；
2.设抛物线的对称轴与x轴交于点D，将∠DCB绕点C按顺时针方向旋转，角的两边CD和CB与x轴分别交于点P、Q，设旋转角为
（0°＜＜90°)
①当等于多少度时，△CPQ是等腰三角形？
②设
，求s与t之间的函数关系式．
如图，在平面直角坐标系xOy中，抛物线与x轴交于A（1，0）、B（5，0）两点．
1.求抛物线的解析式和顶点C的坐标；
2.设抛物线的对称轴与x轴交于点D，将∠DCB绕点C按顺时针方向旋转，角的两边CD和CB与x轴分别交于点P、Q，设旋转角为（0°＜＜90°)
①当等于多少度时，△CPQ是等腰三角形？
②设，求s与t之间的函数关系式．
1.解：（1）根据题意，得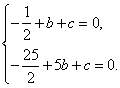 
解得
∴
=
∴顶点C的坐标为（3，2）
2.①∵CD=DB=AD=2，CD⊥AB， ∴∠DCB=∠CBD=45°．……………（4分）
ⅰ）若CQ=CP，则∠PCD=∠PCQ=22.5°．
∴当=22.5°时，△CPQ是等腰三角形．……………（5分）
ⅱ）若CQ=PQ，则∠CPQ=∠PCQ=45°，
此时点Q与D重合，点P与A重合．
∴当=45°时，△CPQ是等腰三角形．……………（6分）
ⅲ）若PC=PQ， ∠PCQ=∠PQC=45°，此时点Q与B重合，点P与D重合．
∴=0°，不合题意．
∴当=22.5°或45°时，△CPQ是等腰三角形．………（7分）
② 连接AC，∵AD=CD=2，CD⊥AB，∴∠ACD=∠CAD=，
AC= BC=……………（8分）
ⅰ）当时，∵∠ACQ=∠ACP+∠PCQ=∠ACP+45°．
∠BPC=∠ACP+∠CAD=∠ACP+45°．∴∠ACQ=∠BPC． 又∵∠CAQ=∠PBC=45°，
∴△ACQ∽△BPC．∴．∴AQ·BP=AC·BC=
×
=8……………（9分）
ⅱ）当时，同理可得AQ·BP=AC·BC=8 ∴
．
解析:略