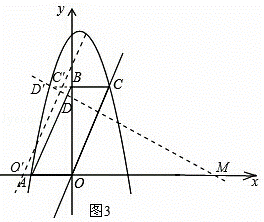
如图，平行四边形ABCD在平面直角坐标系中，点A的坐标为（﹣2，0），点B的坐标为（0，4），抛物线y=﹣x2+mx+n经过点A和C．
（1）求抛物线的解析式．
（2）该抛物线的对称轴将平行四边形ABCO分成两部分，对称轴左侧部分的图形面积记为S1，右侧部分图形的面积记为S2，求S1与S2的比．
（3）在y轴上取一点D，坐标是（0，），将直线OC沿x轴平移到O′C′，点D关于直线O′C′的对称点记为D′，当点D′正好在抛物线上时，求出此时点D′坐标并直接写出直线O′C′的函数解析式．
如图，平行四边形ABCD在平面直角坐标系中，点A的坐标为（﹣2，0），点B的坐标为（0，4），抛物线y=﹣x2+mx+n经过点A和C．
（1）求抛物线的解析式．
（2）该抛物线的对称轴将平行四边形ABCO分成两部分，对称轴左侧部分的图形面积记为S1，右侧部分图形的面积记为S2，求S1与S2的比．
（3）在y轴上取一点D，坐标是（0，），将直线OC沿x轴平移到O′C′，点D关于直线O′C′的对称点记为D′，当点D′正好在抛物线上时，求出此时点D′坐标并直接写出直线O′C′的函数解析式．
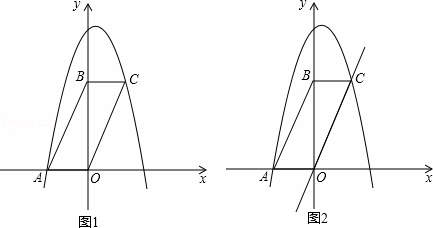
解：（1）如图1，
∵四边形ABCO是平行四边形，
∴BC=OA，BC∥OA．
∵A的坐标为（﹣2，0），点B的坐标为（0，4），
∴点C的坐标为（2，4）．
∵抛物线y=﹣x2+mx+n经过点A和C．
∴
．
解得：
．
∴抛物线的解析式为y=﹣x2+x+6．
（2）如图1，
∵抛物线的解析式为y=﹣x2+x+6．
∴对称轴x=﹣
=，
设OC所在直线的解析式为y=ax，
∵点C的坐标为（2，4），
∴2a=4，即a=2．
∴OC所在直线的解析式为y=2x．
当x=时，y=1，则点F为（，1）．
∴S2=EC•EF
=×（2﹣）×（4﹣1）=．
∴S1=S四边形ABCO﹣S2=2×4﹣=
．
∴S1：S2=： =23：9．
∴S1与S2的比为23：9．
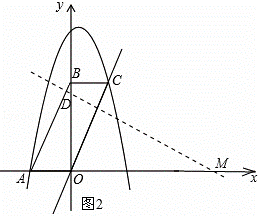
（3）过点D作DM⊥CO，交x轴于点M，如图2，
∵点C的坐标为（2，4），
∴tan∠BOC=．
∵∠OMD=90°﹣∠MOC=∠BOC，
∴tan∠OMD=
=．
∵点D的坐标是（0，），
∴
=，即OM=7．
∴点M的坐标为（7，0）．
设直线DM的解析式为y=kx+b，
则有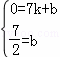
，
解得：
∴直线DM的解析式为y=﹣x+．
∵点D与点D′关于直线O′C′对称，
∴DD′⊥O′C′，且DD′的中点在直线O′C′上．
∵OC∥O′C′，∴DD′⊥OC．
∴点D′是直线DM与抛物线的交点．
联立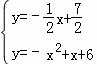
解得：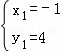
，
，
∴点D′的坐标为（﹣1，4）或（，）．
设直线O′C′的解析式为y=2x+c，
①当点D′的坐标为（﹣1，4）时，如图3，
线段DD′的中点为（
，
）即（﹣，
），
则有2×（﹣）+c=，
解得：c=
．
此时直线O′C′的解析式为y=2x+．
②当点D′的坐标为（，）时，如图4，
同理可得：此时直线O′C′的解析式为y=2x+．
综上所述：当点D′的坐标为（﹣1，4）时，直线O′C′的解析式为y=2x+
；当点D′的坐标为（，）时，直线O′C′的解析式为y=2x+．
