已知函数
（
＞0，≠1，
≠﹣1），是定义在（﹣1，1）上的奇函数.
（1）求实数的值；
（2）当=1时，判断函数
在（﹣1，1）上的单调性，并给出证明；
（3）若
且
，求实数
的取值范围.
已知函数（＞0，≠1，≠﹣1），是定义在（﹣1，1）上的奇函数.
（1）求实数的值；
（2）当=1时，判断函数在（﹣1，1）上的单调性，并给出证明；
（3）若且，求实数的取值范围.
解：（1）∵函数是奇函数，∴
∴
∴
；∴
∴
， 2分
整理得
对定义域内的
都成立．∴
．
所以
或
（舍去）∴． 4分
（2）由（1）可得
；令
设
，则
6分
∵∴
，
∴
．
I. 当
时，
，即
．
∴当时，在（﹣1，1）上是减函数． 8分
II. 当
时，
，即
．
∴当时，在（﹣1，1）上是增函数． 9分
（3）∵
， ∴，
由
，得
，
∵函数是奇函数， ∴
， 10分
故由（2）得在（﹣1，1）上是增函数，∴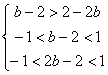
11分
解得
∴实数的取值范围是
。 12分