(07年北京卷文)(本小题共14分)
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 的直二面角.
的直二面角.![]() 是
是![]() 的中点.
的中点.
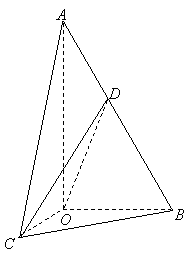
(I)求证:平面![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
(07年北京卷文)(本小题共14分)
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 的直二面角.
的直二面角.![]() 是
是![]() 的中点.
的中点.

(I)求证:平面![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
解析:解法一:
(I)由题意,![]() ,
,![]() ,
,
![]() 是二面角
是二面角![]() 是直二面角,
是直二面角,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
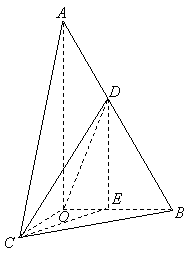
(II)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() (如图),则
(如图),则![]() ,
,
![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
又![]() .
.
![]() 在
在![]() 中,
中,![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
解法二:
(I)同解法一.
(II)建立空间直角坐标系![]() ,如图,
,如图,
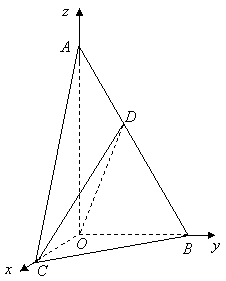
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
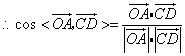
![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.