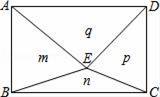
如图，E是矩形ABCD内的一个动点，连接EA、EB、EC、ED，得到△EAB、△EBC、△ECD、△EDA，设它们的面积分别是m、n、p、q，给出如下结论：
①m+n=q+p；
②m+p=n+q；
③若m=n，则E点一定是AC与BD的交点；
④若m=n，则E点一定在BD上．
其中正确结论的序号是（ ）
A．①③ B．②④ C．①②③ D．②③④
如图，E是矩形ABCD内的一个动点，连接EA、EB、EC、ED，得到△EAB、△EBC、△ECD、△EDA，设它们的面积分别是m、n、p、q，给出如下结论：
①m+n=q+p；
②m+p=n+q；
③若m=n，则E点一定是AC与BD的交点；
④若m=n，则E点一定在BD上．
其中正确结论的序号是（ ）
A．①③ B．②④ C．①②③ D．②③④
B【考点】矩形的性质．
【分析】过E作MN⊥AB，交AB于M，CD于N，作GH⊥AD，交AD于G，BC于H，由矩形的性质容易证出①不正确，②正确；若m=n，则p=q，作AP⊥BE于P，作CQ⊥DE于Q，延长BE交CD于F，先证AP=CQ，再证明△ABP≌△CFQ，得出AB=CF，F与D重合，得出③不正确，④正确，即可得出结论．
【解答】解：过E作MN⊥AB，交AB于M，CD于N，作GH⊥AD，交AD于G，BC于H，如图1所示：
则m=
ABEM，n=BCEH，p=
CDEN，q=ADEG，
∵四边形ABCD是矩形，
∴AB=CD=GH，BC=AD=MN，
∴m+p=ABMN=ABBC，n+q=（BCGH=BCAB，
∴m+p=n+q；
∴①不正确，②正确；
若m=n，则p=q，作AP⊥BE于P，作CQ⊥DE于Q，延长BE交CD于F，如图2所示：
则∠APB=∠CQF=90°，
∵m=BEAP，n=BECQ，
∵m=n，
∴AP=CQ，
∵AB∥CD，
∴∠1=∠2，
在△ABP和△CFQ中，
，
∴△ABP≌△CFQ（AAS），
∴AB=CF，
∴F与D重合，
∴E一定在BD上；
∴③不正确，④正确．
故选：B．
【点评】本题考查了矩形的性质、三角形面积的计算、全等三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等是解决问题的关键．