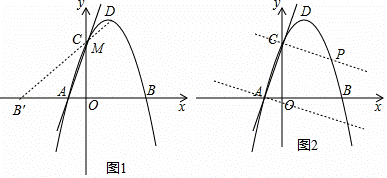
如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3![]() ,0)两点,与y轴交于点C,点D是该抛物线的顶点.
,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
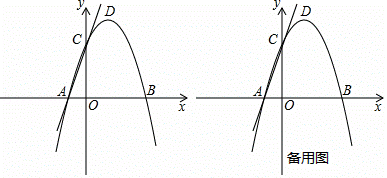
如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3![]() ,0)两点,与y轴交于点C,点D是该抛物线的顶点.
,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

解:(1)设抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
当x=0时,y=﹣x2+2x+3=3,则C(0,3),
设直线AC的解析式为y=px+q,
把A(﹣1,0),C(0,3)代入得![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=3x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4),
作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),
∵MB=MB′,
∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,
而BD的值不变,
∴此时△BDM的周长最小,
易得直线DB′的解析式为y=x+3,
当x=0时,y=x+3=3,
∴点M的坐标为(0,3);
(3)存在.
过点C作AC的垂线交抛物线于另一点P,如图2,
∵直线AC的解析式为y=3x+3,
∴直线PC的解析式可设为y=﹣![]() x+b,
x+b,
把C(0,3)代入得b=3,
∴直线PC的解析式为y=﹣![]() x+3,
x+3,
解方程组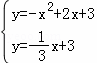 ,解得
,解得![]() 或
或![]() ,则此时P点坐标为(
,则此时P点坐标为(![]() ,
,![]() );
);
过点A作AC的垂线交抛物线于另一点P,直线PC的解析式可设为y=﹣![]() x+b,
x+b,
把A(﹣1,0)代入得![]() +b=0,解得b=﹣
+b=0,解得b=﹣![]() ,
,
∴直线PC的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
解方程组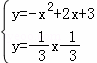 ,解得
,解得![]() 或
或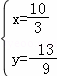 ,则此时P点坐标为(
,则此时P点坐标为(![]() ,﹣
,﹣![]() ),
),
综上所述,符合条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),
),