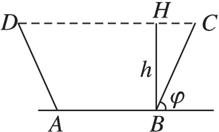
（1）若渠中流水的横断面积为S，水面的高为h，当水渠侧边的倾斜角φ为多大时，才能使横断面被水浸湿的周长为最小？
（2）若被水浸湿的水渠侧边和水渠底面边长都等于a，当水渠侧边倾斜角φ多大时，水流的横断面积为最大？
（1）若渠中流水的横断面积为S，水面的高为h，当水渠侧边的倾斜角φ为多大时，才能使横断面被水浸湿的周长为最小？
（2）若被水浸湿的水渠侧边和水渠底面边长都等于a，当水渠侧边倾斜角φ多大时，水流的横断面积为最大？
解：
（1）依题意,侧边BC=h·（sinφ）-1,设下底AB=x,则上底CD=x+2hcotφ,又s=
（2x+2hcotφ）h=（x+hcotφ）h,
∴下底x=
-hcotφ,
∴横断面被水浸湿周长l=
+（
-hcotφ）=
-
+
（0＜φ＜
）.
∴l′φ=
+
.
令l′φ=0，解得
cosφ=
,∴φ=
.
根据实际问题的意义，当φ=
时，水渠横断面被水浸湿的周长最小.
（2）设水渠高为h,水流横断面积为S,则
S=
（a+a+2acosφ）·h=
（2a+2acosφ）·asinφ=a2（1+cosφ）·sinφ（0＜φ＜
）.
∴S′=a2［-sin2φ+（1+cosφ）cosφ］
=a2（2cosφ-1）（cosφ+1）.
令S′=0，得cosφ=
或cosφ=-1（舍），故在（0,
）内，当φ=
时，水流横断面积最大，最大值为
S=a2（1+cos
）sin
=
a2.