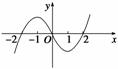
设f(x)是一个三次函数，f′(x)为其导函数，如图所示的是y＝x·f′(x)的图象的一部分，则f(x)的极大值与极小值分别是( )
A．f(1)与f(－1) B．f(－1)与f(1)
C．f(－2)与f(2) D．f(2)与f(－2)
设f(x)是一个三次函数，f′(x)为其导函数，如图所示的是y＝x·f′(x)的图象的一部分，则f(x)的极大值与极小值分别是( )
A．f(1)与f(－1) B．f(－1)与f(1)
C．f(－2)与f(2) D．f(2)与f(－2)
C
解析 由图象知f′(2)＝f′(－2)＝0.
∵x>2时，y＝x·f′(x)>0，∴f′(x)>0，
∴y＝f(x)在(2，＋∞)上单调递增；
同理，f(x)在(－∞，－2)上单调递增，在(－2,2)上单调递减，
∴y＝f(x)的极大值为f(－2)，极小值为f(2)，故选C.