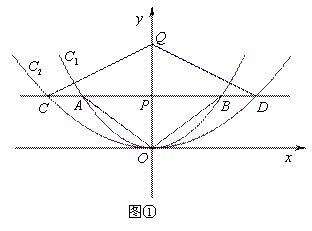
如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在
轴正半轴上，过点P作平行于
轴的
直线，分别交抛物线C1：
于点A、B，交抛物线C2：
于点C、D.原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD.
猜想与证明 填表：
| m | 1 | 2 | 3 |
|
|
|
由上表猜想：对任意m（m＞0）均有
= .请证明你的猜想.
探究与应用 （1）利用上面的结论，可得⊿AOB与⊿CQD面积比为 ；
（2）当⊿AOB和⊿CQD中有一个是等腰直角三角形时，求⊿CQD与⊿AOB面积之差；
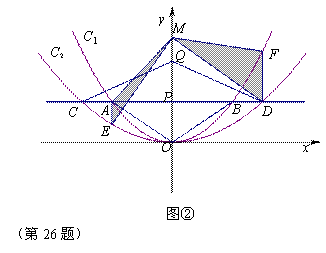
联想与拓展 如图②过点A作轴的平行线交抛物线C2于点E，过点D作轴的平行线交抛物线C1于点F.在轴上任取一点M，连接MA、ME、MD和MF，则⊿MAE与⊿MDF面积的比值为 .
 | |||
 | |||
