如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,
如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
【小题1】小岛D和小岛F相距多少海里?
【小题2】已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
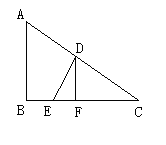
【小题1】连结DF,则DF⊥BC
∵AB⊥BC,AB=BC=200海里.
∴AC=
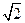
AB=200
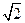
海里,∠C=45°
∴CD=
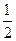
AC=100
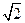
海里
DF=CF,
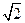
DF=CD
∴DF=CF=

CD=

×100
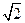
=100(海里)
所以,小岛D和小岛F相距100海里.
【小题2】设相遇时补给船航行了x海里,那么DE=x海里,AB+BE=2x海里,
EF=AB+BC-(AB+BE)-CF=(300-2x)海里
在Rt△DEF中,根据勾股定理可得方程
x
2=100
2+(300-2x)
2整理,得3x
2-1200x+100000=0解析:
p;【解析】略


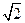 AB=200
AB=200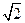 海里,∠C=45°
海里,∠C=45°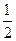 AC=100
AC=100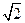 海里
海里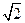 DF=CD
DF=CD CD=
CD= ×100
×100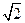 =100(海里)
=100(海里)