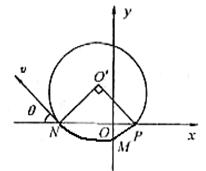
（09年滨海新区重点学校联考）（15分） 如图所示，在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场，第三象限内有沿y轴负方向的匀强电场，第四象限内无电场和磁场。质量为m、带电量为q的粒子从M点以速度
沿x轴负方向进入电场，不计粒子的重力，粒子经N和x轴上的P点最后又回到M点。设
，求：
（1）电场强度E的大小。
（2）匀强磁场的磁感应强度B的大小和方向。
（3）粒子从M点进入电场，经N、P点最后又回到M点所用的总时间。
（09年滨海新区重点学校联考）（15分） 如图所示，在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场，第三象限内有沿y轴负方向的匀强电场，第四象限内无电场和磁场。质量为m、带电量为q的粒子从M点以速度沿x轴负方向进入电场，不计粒子的重力，粒子经N和x轴上的P点最后又回到M点。设，求：
（1）电场强度E的大小。
（2）匀强磁场的磁感应强度B的大小和方向。
（3）粒子从M点进入电场，经N、P点最后又回到M点所用的总时间。
解析：
（1）根据粒子在电场中运动的情况可知，粒子带负电，粒子在电场中运动所用的时间设为
x方向：
，y方向：
解得：电场强度
（2）设到达N点的速度v，运动方向与x轴负方向的夹角为θ，如图所示。
由动能定理得：
将代入得：
因为
，所以
粒子在磁场中做匀速圆周运动，经过P点时速度方向也与x负方向成45°，从到M作直线运动OP＝OM＝L，所以
。
粒子在磁场中的轨道半径为
洛仑兹力充当向心力，根据牛顿第二定律有
得
联立解得：
，方向垂直纸面向里。
（3）粒子在电场中运动的时间为
设粒子在磁场中运动所用的时间为
，有
从P离开磁场作匀速直线运动到M所用的时间为
粒子从M点进入电场，经N、P点最后又回到M点所用的时间为：
