(本小题满分16分)
已知函数
和函数
，记
．
（1）当
时，若
在
上的最大值是
，求实数
的取值范围；
（2）当
时，判断
在其定义域内是否有极值，并予以证明；
（3）对任意的
，若在其定义域内既有极大值又有极小值，试求实数的取值范围．
(本小题满分16分)
已知函数和函数，记．
（1）当时，若在上的最大值是，求实数的取值范围；
（2）当时，判断在其定义域内是否有极值，并予以证明；
（3）对任意的，若在其定义域内既有极大值又有极小值，试求实数的取值范围．
(本小题满分16分)解：（1）
时，
．
①当
时，
，不合题意；
②当
时，
在
上递增，在
上递减，而
，故不合题意；
③当
时，
在
上递减，在
上递增，
在
上的最大值是
，所以
，即
，所以
．
综上所述，实数
的取值范围是
．
（2）
时，
定义域为
，
．
①当
时，
，
在
上单调递增，从而在其定义域内没有极值；
②当
时，
，令
有
，但是
时，，单调递增，
时，，也单调递增，所以在其定义域内也没有极值．
综上，在其定义域内没有极值．
（3）据题意可知，令
，即方程
在上恒有两个不相等的实数根．即
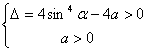恒成立，因为
，
，所以
．