（本小题满分14分）已知函数
.
（Ⅰ）试判断函数f (x)的单调性并说明理由；
（Ⅱ）若对任意的
，不等式组
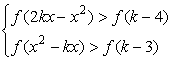恒成立，求实数k的取值范围。
（本小题满分14分）已知函数.
（Ⅰ）试判断函数f (x)的单调性并说明理由；
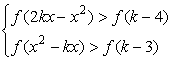（Ⅱ）若对任意的，不等式组恒成立，求实数k的取值范围。
（1）函数f (x)在R上单调递增. 2分
利用导数证明如下：
因为
，
所以，
在R上恒成立，所以f (x)在R上递增. 4分
（2）由于f (x)在R上递增，不等式组可化为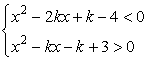
，对于任意x∈[0，1]恒成立. 6分
令
对任意x∈[0，1]恒成立，
必有
，即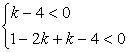
，解之得-3<k<4， 9分
再由
对任意x∈[0，1]恒成立可得
，
在x∈[0，1]恒成立，因此只需求
的最小值，而
当且仅当x=1时取等号，故k<2. 12分
综上可知，k的取值范围是（-3，2）. 14分