,θ∈(0,π),求cotθ的值. 
,θ∈(0,π),求cotθ的值. 解析一:由sinθ+cosθ=,得(sinθ+cosθ)2=
,
∴sinθ·cosθ=-
＜0.
而θ∈(0,π),∴90°＜θ＜180°,sinθ＞0,cosθ＜0,sinθ-cosθ＞0.
∴(sinθ-cosθ)2=1-2sinθcosθ=
.
∴sinθ-cosθ=
.
由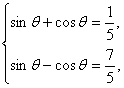
得
sinθ=
,cosθ=-
,cotθ=-
.
解析二:由sinθ+cosθ=
,可得
cos2θ=(
-sinθ)2,
即1-sin2θ=(
-sinθ)2,
整理得25sin2θ-5sinθ-12=0,
(5sinθ-4)(5sinθ+3)=0,
解得sinθ=
或sinθ=-
.
由0＜θ＜π知,sinθ=-
不合题意,
∴sinθ=
,cosθ=
-sinθ=-
.
∴cotθ=-
.
解析三:同解析一得sinθ·cosθ=-
,
∴
=-
.
等式两边同除以cos2θ,得
=-
,
整理得12tan2θ+25tanθ+12=0,
解得tanθ=-
或tanθ=-
.
∵sinθcosθ＜0,sinθ+cosθ=
＞0,θ∈(0,π),
∴|sinθ|＞|cosθ|.∴|tanθ|＞1.
∴tanθ＜-1或tanθ＞1(舍去).
∴cotθ＞-1.
∴cotθ=-
.
点评:对于三角函数式sinα+cosα、sinα-cosα、sinαcosα,它们之间可通过(sinα+cosα)2=1+2sinαcosα,(sinα-cosα)2=1-2sinαcosα进行转换.若已知sinα+cosα,sinα-cosα,sinα·cosα中三者之一,可求其余两个函数式:如设sinα+cosα=t,则sinα·cosα=
(t2-1),sin3α+cos3α=
t(3-t2),sin4α+cos4α=(sin2α+cos2α)2-2sin2α·cos2α=1-
(t2-1)2.这样利用方程的思想解三角题在三角函数中应用比较广泛.