如图，△ABO的顶点A在函数y＝
（x＞0）的图象上，∠ABO＝90°，过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q．若四边形MNQP的面积为3，则k的值为（ ）
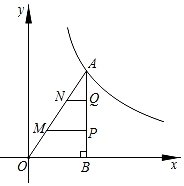
A．9 B．12 C．15 D．18
如图，△ABO的顶点A在函数y＝（x＞0）的图象上，∠ABO＝90°，过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q．若四边形MNQP的面积为3，则k的值为（ ）
A．9 B．12 C．15 D．18
D
【分析】易证△ANQ∽△AMP∽△AOB，由相似三角形的性质：面积比等于相似比的平方可求出△ANQ的面积，进而可求出△AOB的面积，则k的值也可求出．
解：
∵NQ∥MP∥OB，
∴△ANQ∽△AMP∽△AOB，
∵M、N是OA的三等分点，
∴
＝
，
＝
，
∴
＝
，
∵四边形MNQP的面积为3，
∴
＝，
∴S△ANQ＝1，
∵
＝（）2＝
，
∴S△AOB＝9，
∴k＝2S△AOB＝18，
故选：D．