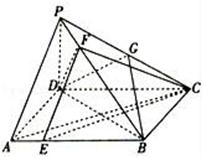
如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，PA⊥PC，底面ABCD为菱形，G为PC中点，E、F分别为AB、PB上一点，△BCE的面积为6
，PB=4PF．
（1）求证：AC⊥DF；
（2）求证：EF∥平面BDG；
（3）求三棱锥B﹣CEF的体积．
如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，PA⊥PC，底面ABCD为菱形，G为PC中点，E、F分别为AB、PB上一点，△BCE的面积为6，PB=4PF．
（1）求证：AC⊥DF；
（2）求证：EF∥平面BDG；
（3）求三棱锥B﹣CEF的体积．
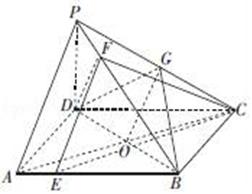【解答】（1）证明：∵PD⊥平面ABCD，∴PD⊥AC…
∵底面ABCD为菱形，∴AC⊥BD，…
∵BD∩PD=D，∴AC⊥平面PBD，…
又DF⊂平面PBD，∴AC⊥DF…
（2）证明：∵AB=4AE，PB=4PF，∴EF∥PA，…
设AC与BD的交点为O，连接OG，∵ABCD为菱形，
∴O为AC中点，又G为PC中点，∴OG∥PA，…
∴EF∥OG，又EF⊄平面BDG，OG⊂平面BDG，∴EF∥平面BDG…
（3）解：
设PD=m，∵PD⊥平面ABCD，∴PD⊥AD，PD⊥CD，…
又
，
∴
，
∵PA⊥PC，∴2（m2+32）=16×6，∴m=4…
∵PB=4PF，∴F到平面ABCD的距离为
…
∵△BCE的面积为
，
∴
…