（1）为使导体棒cd也能随ab棒而运动，问μ最大不能超过多大？
（2）若以上条件已满足，求导体棒cd所能达到的最大速度v2；
（3）当导体棒cd以恒定的速度运动时，求作用在导体棒ab上的拉力大小及其单位时间做的功；
（4）当导体棒cd以恒定的速度运动时，此时电路中的电功率大小和焦耳热功率大小各为多少？
（4）当导体棒cd以恒定的速度运动时，此时电路中的电功率大小和焦耳热功率大小各为多少？
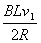
得：
<
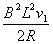
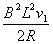
, 所以μ最大不能超过 （2）设cd棒速度为v时电路中电流为I，有I=
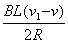
，对cd棒受力分析，由牛顿第二定律，有：BIL－μmg=ma 显然ｖ越大a越小，故当a=0时cd棒有最大速度v2，那么v2=v1－
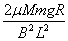
（3）当cd棒以稳定速度运动时，电路中的感应电流为 I=
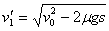
则为使ab棒匀速成运动，作用在ab棒上的水平拉力F应为F=BIL+μmg=2μmg，其功 率应为P1=2μmgv1.（4）此时电路的电功率及焦耳热功率相等，为P=I2×2R=
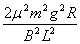
注：（1）4分； （2）6分； （3）6分： （4）4分。