△ABC为等腰直角三角形，OA=1，OC为斜边AB上的高，P为线段OC的中点，则
=________
△ABC为等腰直角三角形，OA=1，OC为斜边AB上的高，P为线段OC的中点，则=________
．
【考点】平面向量数量积的运算．
【专题】数形结合；向量法；平面向量及应用．
【分析】可分别以CB，CA两直线为x轴，y轴，建立平面直角坐标系，根据条件容易求出CA=CB=
，从而可确定图形上各点的坐标，从而得出向量
的坐标，然后进行数量积的坐标运算即可．
【解答】解：如图，分别以边CB，CA所在直线为x，y轴，建立如图所示平面直角坐标系；
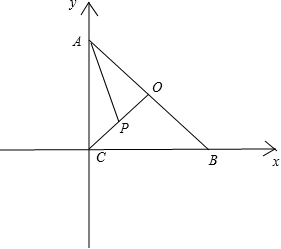根据条件知CA=CB=
；
∴A（0，），B（，0），O（
），P（
）；
∴
；
∴
．
故答案为：
．
【点评】考查建立平面直角坐标系，利用向量坐标解决向量问题的方法，建立完坐标系能够求出图形上点的坐标，从而求出向量的坐标，向量数量积的坐标运算．