如图,在等腰直角三角形OPQ中,∠POQ=90°,OP=2![]() ,点M在线段PQ上.
,点M在线段PQ上.
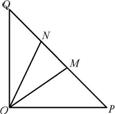
(例4)
(1)若OM=![]() ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
如图,在等腰直角三角形OPQ中,∠POQ=90°,OP=2![]() ,点M在线段PQ上.
,点M在线段PQ上.

(例4)
(1)若OM=![]() ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
(1)在△OMP中,∠P=45°,OM=![]() ,OP=2
,OP=2![]() .
.
由余弦定理,得OM2=OP2+PM2-2×OP×PM×cos 45°,
得PM2-4PM+3=0,解得PM=1或PM=3.
(2)设∠POM=α,0°≤α≤60°,在△OMP中,由正弦定理,得![]() =
=![]() ,
,
所以OM=![]() ,同理ON=
,同理ON=![]() ,
,
故S△OMN=![]() ×OM×ON×sin ∠MON
×OM×ON×sin ∠MON
=![]() ×
×![]()
=![]()
=

=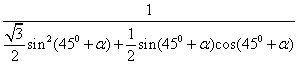
=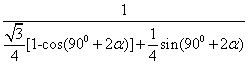
= =
= .
.
因为0°≤α≤60°,所以30°≤2α+30°≤150°.
所以当α=30°时,sin(2α+30°)取得最大值为1,此时△OMN的面积取得最小值,即∠POM=30°时,△OMN的面积最小,其最小值为8-4![]() .
.