如图，矩形
中，E为边
上一点，将
沿
折叠，使点A的对应点F恰好落在边
上，连接
交于点N，连接
．若
，
，则矩形的面积为________．
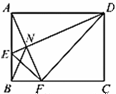
如图，矩形中，E为边上一点，将沿折叠，使点A的对应点F恰好落在边上，连接交于点N，连接．若，，则矩形的面积为________．
【解析】
根据折叠的性质以及矩形的性质推导出
，故
，在
中应用勾股定理，得到
，即可求解．
【详解】
解：由折叠可得：
，
，
，
∴
∵
，
且易得
，
∴
，
∴
，
∵
，
，
∴，
∴
，即，
在中，
，
解得，
∵，
∴
，
故答案为：．
【点睛】
本题考查折叠的性质，矩形的性质，勾股定理等内容，解题的关键是不求出线段的具体长度，而是得到AB和BF的比例关系直接求解矩形的面积．