已知关于 的函数 ， （I）试求函数的单调区间； （II）若在区间 内

已知关于 的函数 ，

（I）试求函数的单调区间；

（II）若在区间 内有极值，试求a的取值范围；

（III） 时，若有唯一的零点 ，试求 .（注：为取整函数，表示不超过的最大整数，如 ；以下数据供参考：

【分析】

（I）由题意的定义域为 ，对a分类讨论：当a≥0时，当a＜0时，即可得出单调性；
（II） , 所以的定义域也为，且，

令h（x）=2x³-ax-2，x∈[0，+∞），h′（x）=6x²-a，当a＜0时，可得：函数h（x）在（0，1）内至少存在一个变号零点x₀，且x₀也是f′（x）的变号零点，此时f（x）在区间（0，1）内有极值．当a≥0时，由于函数f（x）单调，因此函数f（x）无极值．

（III）a＞0时，由（II）可知：f（1）=3知x∈（0，1）时，f（x）＞0，因此x₀＞1．又f′（x）在区间（1，+∞）上只有一个极小值点记为x₁，由题意可知：x₁即为x₀．得到 ，即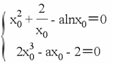 ，消去可得： ，a＞0，令 分别研究单调性即可得出x₀的取值范围．

【详解】（I）由题意的定义域为  

（i）若，则在上恒成立，为其单调递减区间；

（ii）若，则由得，

时，，时，，

所以为其单调递减区间；为其单调递增区间；

（II）    所以的定义域也为，

且

令 (*)

则 (**)

（i）当时, 恒成立,所以为上的单调递增函数，

又，所以在区间内存在唯一一个零点，

由于为上的单调递增函数，所以在区间内，

从而在，所以此时在区间内有唯一极值且为极小值，适合题意,

（ii）当时,即在区间(0,1)上恒成立,此时, 无极值.

综上所述,若在区间内有极值，则a的取值范围为.

(III) ,由（II）且知时, .

由(**)式知，。

由于，所以，

又由于，

所以

亦即 ，

由

从而得

所以，,

从而，又因为有唯一的零点，所以 即为,

消去a,得

时令,

则在区间上为单调递增函数, 为单调递减函数,

且

【点睛】