如图，在平面直角坐标系中，直线L：y=-2x-8分别与x轴、y轴相交于A、B两点，点P(0,k)是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P。
（1）连结PA，若PA=P
B，试判断⊙P与X轴的位置关系，并说明理由；
（2）当K为何值时，以⊙P
与直线L的两个交点和圆心P为顶点的三角形是正三角形？
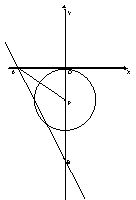
如图，在平面直角坐标系中，直线L：y=-2x-8分别与x轴、y轴相交于A、B两点，点P(0,k)是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P。
（1）连结PA，若PA=PB，试判断⊙P与X轴的位置关系，并说明理由；
（2）当K为何值时，以⊙P与直线L的两个交点和圆心P为顶点的三角形是正三角形？
（１）由直线L的解析式可知A（-4，0），B（0，-8）
设OP=X，则BP=8-X，AP=8-X
由勾股定理得 X2 + 42 =（8-X）2
解得 X = 3 -
∴ OP = R = 3
∴⊙P与X轴相切
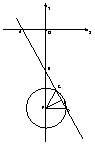
（2）分两种情况讨论：
①当圆心P在线段OB上
由⊿AOB ∽ ⊿PEB得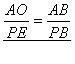 
把AO=4，AB=4
，PE=
代入比例式得 PB=
--------------------3分
∴ OP = 8－ ∴ K = －8 -----2分
②当圆心P在线段OB的延长线上时：
由⊿AOB ∽ ⊿PEB同样可得 PB=
∴ OP = 8 ＋ ∴ K = －－8 （2分）
∴当K=－8或－－8时，以⊙P与直线L的两个交点和圆心P为顶点的三角形是正三角形。 --------------1分