在每个小正方形的边长为1的网格中．点A，B，C，D均在格点上，点E、F分别为线段BC、DB上的动点，且BE=DF．
（Ⅰ）如图①，当BE=
时，计算AE+AF的值等于______
（Ⅱ）当AE+AF取得最小值时，请在如图②所示的网格中，用无刻度的直尺，画出线段AE，AF，并简要说明点E和点F的位置如何找到的（不要求证明）______．
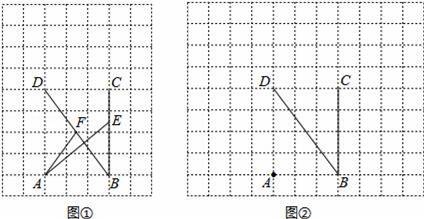
在每个小正方形的边长为1的网格中．点A，B，C，D均在格点上，点E、F分别为线段BC、DB上的动点，且BE=DF．
（Ⅰ）如图①，当BE=时，计算AE+AF的值等于______
（Ⅱ）当AE+AF取得最小值时，请在如图②所示的网格中，用无刻度的直尺，画出线段AE，AF，并简要说明点E和点F的位置如何找到的（不要求证明）______．
【解答】解：（1）根据勾股定理可得：DB=
，
因为BE=DF=
，
所以可得AF=
=2.5，
根据勾股定理可得：AE=
，所以AE+AF=
，
故答案为：
；
（2）如图，
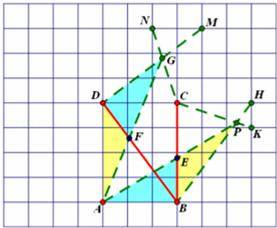
首先确定E点，要使AE+AF最小，根据三角形两边之和大于第三边可知，需要将AF移到AE的延长线上，因此可以构造全等三角形，首先选择格点H使∠HBC=∠ADB，其次需要构造长度BP使BP=AD=4，根据勾股定理可知BH=
=5，结合相似三角形选出格点K，根据
，得BP=
BH=
=4=DA，易证△ADF≌△PBE，因此可得到PE=AF，线段AP即为所求的AE+AF的最小值；同理可确定F点，因为AB⊥BC，因此首先确定格点M使DM⊥DB，其次确定格点G使DG=AB=3，此时需要先确定格点N，同样根据相似三角形性质得到
，得DG=
DM=×5=3，易证△DFG≌△BEA，因此可得到AE=GF，故线段AG即为所求的AE+AF的最小值．
故答案为：取格点H，K，连接BH，CK，相交于点P，连接AP，与BC相交，得点E，取格点M，N连接DM，CN，相交于点G，连接AG，与BD相交，得点F，线段AE，AF即为所求．