(08年厦门外国语学校模拟文)(14分)
已知双曲线的方程为![]() ,离心率为2,过点
,离心率为2,过点![]() 的直线
的直线![]() 交双曲线于不同两点
交双曲线于不同两点![]() 、
、![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)若直线![]() 的倾斜角为
的倾斜角为![]() , 且
, 且![]() ,求
,求![]() ;
;
(Ⅱ)若双曲线的一个焦点为![]() ,求
,求![]() 的取值范围.
的取值范围.
(08年厦门外国语学校模拟文)(14分)
已知双曲线的方程为![]() ,离心率为2,过点
,离心率为2,过点![]() 的直线
的直线![]() 交双曲线于不同两点
交双曲线于不同两点![]() 、
、![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)若直线![]() 的倾斜角为
的倾斜角为![]() , 且
, 且![]() ,求
,求![]() ;
;
(Ⅱ)若双曲线的一个焦点为![]() ,求
,求![]() 的取值范围.
的取值范围.
解析:因为![]() (
(![]() 是双曲线的半焦距)且
是双曲线的半焦距)且![]() ,有
,有![]() ,
,
则双曲线的标准方程可化为![]()
![]() ……………………………(1分)
……………………………(1分)
(Ⅰ)设直线与双曲线的交点为![]()
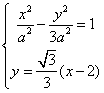 ,有
,有![]() ,则
,则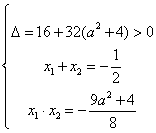
由![]()
有![]() ,有
,有![]() ,则
,则
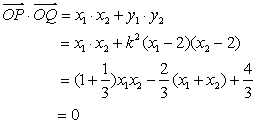 ……………………………(5分)
……………………………(5分)
(Ⅱ)由双曲线的焦点是![]() ,则有
,则有![]() ,又因为
,又因为![]() ,则
,则![]() ,
,
那么双曲线的标准方程为![]() . ……………………………………(6分)
. ……………………………………(6分)
(1)当直线斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
则点![]() 此时
此时![]() .……………………………………(7分)
.……………………………………(7分)
(2)当直线斜率存在时,直线![]() 的方程为
的方程为![]() ,则联立直线与双曲线方程
,则联立直线与双曲线方程
有 , 有
, 有 ![]() ,
,
则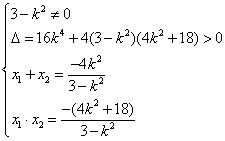 ,…………………………………(9分)
,…………………………………(9分)
那么![]()
![]()
由![]() 有
有![]() , 则
, 则![]()
即![]()
综(1)、(2) 有![]() 的范围是
的范围是![]() ………(14分)
………(14分)