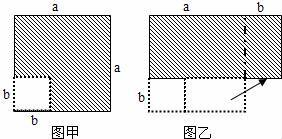
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+2b)(a﹣b)=a2+ab﹣2b2
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+2b)(a﹣b)=a2+ab﹣2b2
C【解答】解:∵图甲中阴影部分的面积=a2﹣b2,图乙中阴影部分的面积=(a+b)(a﹣b),
而两个图形中阴影部分的面积相等,
∴阴影部分的面积=a2﹣b2=(a+b)(a﹣b).