已知三角形ABC的三个顶点均在椭圆
上，且点A是椭圆短轴的一个端点（点A在y轴正半轴上）.
若三角形ABC的重心是椭圆的右焦点，试求直线BC的方程;若角A为
，AD垂直BC于D，试求点D的轨迹方程.
已知三角形ABC的三个顶点均在椭圆上，且点A是椭圆短轴的一个端点（点A在y轴正半轴上）.
若三角形ABC的重心是椭圆的右焦点，试求直线BC的方程;若角A为，AD垂直BC于D，试求点D的轨迹方程.
所求点D的轨迹方程是
1）设B（
,
）,C(
,
),BC中点为(
),F(2,0)
则有
两式作差有
(1)
F(2,0)为三角形重心，所以由
，得
由
得
，
代入（1）得
直线BC的方程为
2)由AB⊥AC得
（2）
设直线BC方程为
，得
，
代入（2）式得
，解得
或
直线过定点（0，
，设D（x,y）
则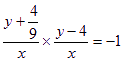
即
所以所求点D的轨迹方程是。