（14分）如图所示，在一次消防演习中，消防员练习使用挂钩从高空

（14分）如图所示，在一次消防演习中，消防员练习使用挂钩从高空沿滑杆由静止滑下，滑杆由AO、OB两段直杆通过光滑转轴连接地O处，可将消防员和挂钩均理想化为质点，且通过O点的瞬间没有机械能的损失。AO长为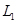=5m，OB长为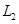=10m。两堵竖直墙的间距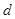=11m。滑杆A端用铰链固定在墙上，可自由转动。B端用铰链固定在另一侧墙上。为了安全，消防员到达对面墙的速度大小不能超过6m/s，挂钩与两段滑杆间动摩擦因数均为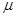=0.8。(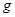=10m/s²，sin37°=0.6，cos37°=0.8)

（1）若测得消防员下滑时，OB段与水平方向间的夹角始终为37°，求消防员在两滑杆上运动时加速度的大小及方向；

（2）若B端在竖直墙上的位置可以改变，求滑杆端点A、B间的最大竖直距离。

（1）在AO段运动的加速度为3.2 m/s²，方向沿AO杆向下；

在OB段运动的加速度为－0.4 m/s²，方向沿BO杆向上。

（2）10.2m

解析:（1）设杆OA、OB与水平方向夹角为α、β，由几何关系：d＝L₁cosα+L₂cosβ（1分）

得出AO杆与水平方向夹角α＝53°    （1分）

由牛顿第二定律得mgsinθ－f＝ma     （1分）

f=μN   N=μmgcosθ  (1分 )

在AO段运动的加速度：a₁＝gsin53°－μgcos53°＝3.2 m/s²，方向沿AO杆向下。（2分）

在OB段运动的加速度：a₂＝gsin37°－μgcos37°＝－0.4 m/s²，方向沿BO杆向上。（2分）

（2）对全过程由动能定理得 mgh－μmgL₁cosα－μmgL₂cosβ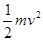＝-0（2分）

其中d＝L₁cosα+L₂cosβ，v ≤6 m/s（1分）

所以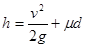：≤ 10.6m（1分）

又因为若两杆伸直，AB间的竖直高度为

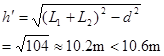  （1分）

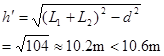所以AB最大竖直距离应为10.2m。（1分）