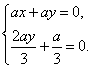(08е№ҙжө·ж·ҖеҢәжңҹдёӯз»ғд№ зҗҶ)пјҲ14еҲҶпјү
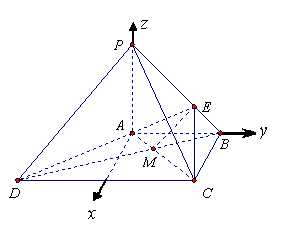
еҰӮеӣҫпјҢеӣӣжЈұй”Ҙ![]() дёӯпјҢ
дёӯпјҢ![]() вҠҘеә•йқў
вҠҘеә•йқў![]() пјҢВ В
пјҢВ В ![]() вҠҘ
вҠҘ![]() пјҺеә•йқў
пјҺеә•йқў![]() дёәжўҜеҪўпјҢ
дёәжўҜеҪўпјҢ![]() пјҢ
пјҢ![]() .
.![]() пјҢзӮ№
пјҢзӮ№![]() еңЁжЈұ
еңЁжЈұ![]() дёҠпјҢдё”
дёҠпјҢдё”![]() пјҺ
пјҺ
пјҲв… пјүжұӮиҜҒпјҡе№ійқў![]() вҠҘе№ійқў
вҠҘе№ійқў![]() пјӣ
пјӣ
пјҲв…ЎпјүжұӮиҜҒпјҡ![]() вҲҘе№ійқў
вҲҘе№ійқў![]() пјӣ
пјӣ
пјҲв…ўпјүжұӮдәҢйқўи§’![]() зҡ„еӨ§е°ҸпјҺ
зҡ„еӨ§е°ҸпјҺ